Tutoriel 7 - Transformations de rotation

Par OGLdev, traduit par DragonJoker

Récupérer les sources

Précédent
Suivant


Introduction

Seconde transformation: la rotation.

Contexte

La prochaine transformation dans notre liste est la rotation, c'est-à-dire que pour un angle et un point donnés, nous voulons tourner le point autour d'un axe. Nous changerons toujours deux des trois coordonnées et laisserons la troisième inchangée. Cela signifie que la transformation se fera sur un des trois plans majeurs : XY (quand on tourne autour de l'axe Z), YZ (quand on tourne autour de l'axe X), XZ (quand on tourne autour de l'axe Y).

Il y a des transformations de rotation plus complexes qui permettent la rotation autour d'un vecteur arbitraire mais nous n'en avons pas encore besoin à cette étape.

Définissons le problème en termes généraux.

Considérons le diagramme suivant :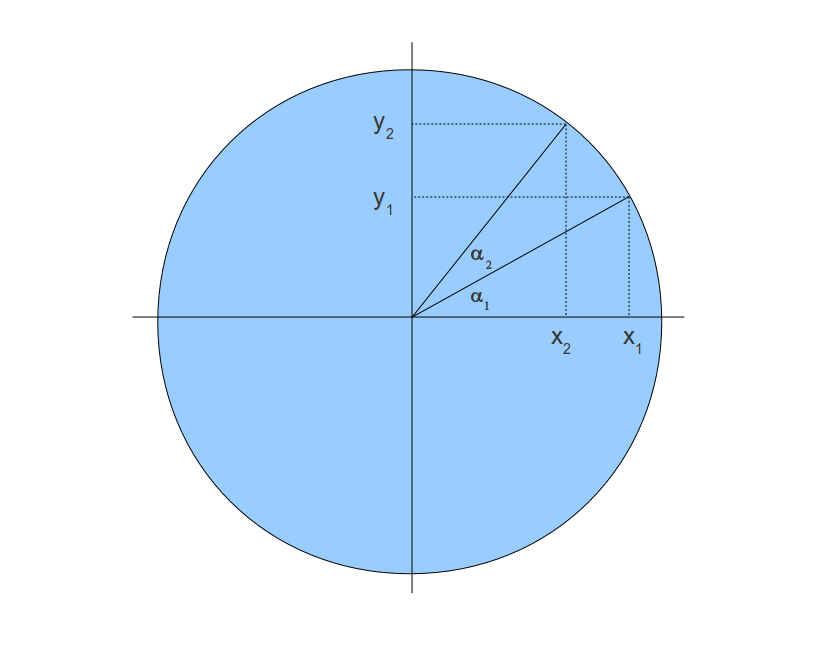


Nous voulons nous déplacer sur le cercle du point (x1, y1) au point (x2, y2). Autrement dit, nous voulons tourner le point (x1, y1) selon l'angle α2.

Supposons que le rayon de ce cercle soit 1, ça signifie donc ceci :

\begin{equation*} x_1 = cos( \alpha_1 )\\ y_1 = sin( \alpha_1 )\\ x_2 = cos( \alpha_1 + \alpha_2 )\\ y_2 = sin( \alpha_1 + \alpha_2 )\\ \end{equation*}

Nous allons utiliser les relations trigonométriques suivantes pour développer x2 et y2 :

\begin{equation*} cos( a + b ) = cos( a ) \times cos( b ) - sin( a ) \times sin( b )\\ sin( a + b ) = sin( a ) \times cos( b ) + cos( a ) \times sin( b ) \end{equation*}

Nous pouvons alors écrire :

\begin{equation*} x_2 = cos( a_1 + a_2 ) = cos( a_1 ) \times cos( a_2 ) - sin( a_1 ) \times sin( a_2 ) = x_1 \times cos( a_2 ) - y_1 \times sin( a_2 )\\ y_2 = sin( a_1 + a_2 ) = sin( a_1 ) \times cos( a_2 ) - cos( a_1 ) \times sin( a_2 ) = y_1 \times cos( a_2 ) + x_1 \times sin( a_2 )\\ \end{equation*}

Dans le diagramme ci-dessus, nous regardons le plan XY et Z pointe dans la page. Si X et Y font partie d'un vecteur 4D alors l'équation ci-dessus peut être écrite sous forme matricielle (sans affecter Z ni W) :

\begin{equation*} \left(\begin{matrix} cos( \alpha ) & -sin( \alpha ) & 0 & 0\\ sin( \alpha ) & cos( \alpha ) & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{matrix}\right) \times \left(\begin{matrix} x\\ y\\ z\\ 1\\ \end{matrix}\right) = \left(\begin{matrix} x \times cos( \alpha ) - y \times sin( \alpha ) &\\ x \times sin( \alpha ) + y \times cos( \alpha ) &\\ z &\\ 1 &\\ \end{matrix}\right) \end{equation*}

Si nous voulons créer des rotations autour des axes X et Y alors les équations sont globalement les mêmes, mais la matrice est organisée de façon un peu différente. Voici la matrice de rotation autour de l'axe Y :

\begin{equation*} \left(\begin{matrix} cos( \alpha ) & 0 & -sin( \alpha ) & 0\\ 0 & 1 & 0 & 0\\ sin( \alpha ) & 0 & cos( \alpha ) & 0\\ 0 & 0 & 0 & 1\\ \end{matrix}\right) \times \left(\begin{matrix} x\\ y\\ z\\ 1\\ \end{matrix}\right) = \left(\begin{matrix} x \times cos( \alpha ) - z \times sin( \alpha ) &\\ y &\\ x \times sin( \alpha ) + z \times cos( \alpha ) &\\ 1 &\\ \end{matrix}\right) \end{equation*}

Et la matrice de rotation autour de l'axe X :

\begin{equation*} \left(\begin{matrix} 1 & 0 & 0 & 0\\ 0 & cos( \alpha ) & -sin( \alpha ) & 0\\ 0 & sin( \alpha ) & cos( \alpha ) & 0\\ 0 & 0 & 0 & 1\\ \end{matrix}\right) \times \left(\begin{matrix} x\\ y\\ z\\ 1\\ \end{matrix}\right) = \left(\begin{matrix} x &\\ y \times cos( \alpha ) - z \times sin( \alpha ) &\\ y \times sin( \alpha ) + z \times cos( \alpha ) &\\ 1 &\\ \end{matrix}\right) \end{equation*}

Explication du code

Les changements de code dans ce tutoriel sont mineurs. Nous changeons uniquement le contenu de la matrice de transformation dans le code C/C++.

World.m[0][0]=cosf(Scale);
World.m[0][1]=-sinf(Scale);
World.m[0][2]=0.0f;
World.m[0][3]=0.0f;
World.m[1][0]=sinf(Scale);
World.m[1][1]=cosf(Scale);
World.m[1][2]=0.0f;
World.m[1][3]=0.0f;
World.m[2][0]=0.0f;
World.m[2][1]=0.0f;
World.m[2][2]=1.0f;
World.m[2][3]=0.0f;
World.m[3][0]=0.0f;
World.m[3][1]=0.0f;
World.m[3][2]=0.0f;
World.m[3][3]=1.0f;

Comme vous pouvez le voir, nous tournons autour de l'axe Z. Vous pouvez essayer les autres rotations, mais je pense qu'à ce stade, sans une vraie projection de la 3D vers la 2D, les autres rotations vont sembler étranges.

Nous les réaliserons dans une classe de pipeline complet de transformation dans les tutoriels à venir.

Remerciements

Merci à Etay Meiri de me permettre de traduire ses tutoriels.

Résultat :
resultat

Article d'origine

Précédent
Suivant